Many articles on quantum computing are rushing quite a lot. “A qubit can be in the states 0 and 1 at the same time, and that’s why quantum computers are better than classical ones.” Sure…? Um, no, that was a bit too quick. In my series “FAQ: Quantum computer” I try to clear up common misconceptions and erase question marks. This article is about how to make a quantum computer out of many qubits.
I divide my FAQ into three parts. In the first part, “From Bit to Qubit”, I explain the basic differences between classical bits and quantum mechanical qubits. Please read that part first if you don’t already know it, as I won’t explain the basic concepts again. This part is all about what it takes to make a quantum computer. What makes a quantum computer so powerful? Can a quantum computer solve every problem in one step? What do we need for a quantum computer? Why is it so hard to build a quantum computer? The third and last part, “From classical to quantum computers”, will deal with how exactly a quantum computer calculates, what a quantum computer is actually good for, and what not.
What makes a quantum computer so powerful?
or: What is quantum parallelism?
It is often said that a quantum computer is better than a classical one because it can overlay many different possibilities and calculate them in just one step. What is referred to here is the so-called quantum parallelism and this is indeed the reason why quantum computers are so powerful. I will deal with the second part concerning “everything in one step” in the next question. First, however, I turn to the ominous quantum parallelism.
A single qubit does not make a quantum computer. As I explained in the last article, a single qubit decays into a bit-like state when measured, and is thus not one bit better than a bit. For a quantum computer to work, multiple qubits must come together.
Classical bits are autonomous, independent beings. One bit does not care what the other one does. This means I can determine the state (1 or 0, switch up or down) of one bit without affecting the next. If I know what state one bit is in, I know nothing about the state of the others. Qubits can also be completely independent of each other. But often they are not. In the quantum world, it is possible for the state of one qubit to depend on the state of another. It’s like with super good friends (or even BFFs): If one is happy, so is the other. If one is pissed off, the other is already lighting the torches.

This symbiosis goes so far that if the first qubit is undecided, the second one cannot decide either. If the first qubit is in a superposition of happy and angry, then the corresponding BFF qubit is in a superposition of happy and angry. This common superposition, this magical connection of BFFs, in which the state of one qubit depends on the other, is what we call entanglement.
There is another way to combine two qubits: the foe constellation. If the first qubit is in state 0 (happy), the foe qubit is in state 1 (angry) and vice versa. And these two can also entangle if they are superimposed. So in total there are four different combinations: 00 (happy friends), 01 (happy qubit, angry foe), 10 (angry qubit, happy foe), and 11 (angry friends). If I cleverly entangle the two qubits, they can be in all four constellations at the same time.

In the entangled state, it is not yet clear in which mood the two qubits are. Both qubits are in a superposition of happy and angry. But if I know how the two qubits have been entangled (e.g. as friends or foes) and if I find out what mood one of the qubits is in, I can always predict with absolute certainty what mood the other is in.
Note: The individual states 00, 01, 10, and 11 are not entangled. We only speak of entanglement when the state of one qubit depends on the state of the other. For example, in the superposition 00 + 11 (friends) or 01 + 10 (foes). It follows that the combination 00 + 01 is not an entangled state. The first qubit is always happy and doesn’t care what the other qubit does.
The lottery experiment
What does this have to do with quantum computers? Let’s imagine that we want to carry out an experiment with two people. Let’s say person A has won the lottery and now meets person B to tell them about it. What will happen? That depends on whether the two are friends or foes and who is angry or happy. If we want to simulate this situation with a normal computer, we have to test all four constellations (happy-happy, happy-angry, angry-happy, angry-angry) one after the other. If we have a quantum computer, we can entangle all four constellations and thus test them in parallel. This is what we call quantum parallelism.
The power of the quantum computer lies in the number of constellations that the system of qubits can take. If I have n qubits, they can assume 2n different states. For n = 2, these are the 4 states shown above (00, 01, 10, 11). For 3 qubits this is already 8 (000, 001, 010, 011, 100, 101, 110, 111). For 4 qubits there are 16. The number grows rapidly, namely exponentially. By the way, a normal computer with 4 bits can also assume 16 different constellations. But this one has to check all 16 constellations one after the other. Only a quantum computer can superimpose the 16 cases and test them simultaneously.
Rice corn to A5
There is a beautiful story that illustrates the extent of this exponential growth. When the game of chess was invented, the emperor of the time wanted to reward the inventor. The emperor said the inventor could make a wish and should not be modest about it. The inventor said: He wanted a grain of rice for the first square of the chessboard. Two grains for the second. And he wanted twice as many grains for every next square as for the previous one. The emperor was offended by this banal wish. But what do you guess: how many grains of rice are on the last square? The formula is the same as for the qubits: 2n. A chessboard has 64 squares, and 263 (the power is 64-1=63 because the row starts with 20 = 1) is 9,223,372,036,864,775,808 – nine trillion. There are a whopping 18 trillion grains of rice on the entire board. 540 billion tonnes of rice. The world’s rice harvest of just under 1000 years.

A quantum computer with 64 qubits can therefore assume nine trillion different states. And test nine trillion initial values simultaneously. Even the best supercomputer would take a while to do that. Let’s hope it has a lot of rice as provisions.
Can a quantum computer solve every problem in one step?
I admit it sounds very much like it, but unfortunately, it is not true. Let’s look at the lottery experiment again. If we have two qubits available, we can associate the four different combinations of qubits (00, 01, 10, 11) with the four constellations of persons (happy-happy, happy-angry, angry-happy, angry-angry). Now we only have to create a superposition of these four states and thus test all four cases simultaneously – the problem is solved in one step. Right? Wrong.
If we run the complicated state 00 + 01 + 10 + 11 through the quantum computer, what do we get? An even more complicated, highly entangled state. But when we try to read out this state, it collapses to one of four possibilities: 00, 01, 10, or 11 (see “How to translate quantum to classical information?” in Part One). What does this tell me about the outcome of the four simultaneous experiments? Nada. Any additional information stored in the entanglement is gone.

Just mindlessly superimposing everything doesn’t work – quantum parallelism alone doesn’t get us anywhere. We can’t just replace normal processors with quantum processors and expect everything to run exponentially faster. We have to guarantee that the measurement result at the end of the simulation will give us useful information. How exactly does that work? Good question.
The sad answer: there is no one-size-fits-all solution. For each problem, we have to come up with a new solution: a kind of cooking recipe for quantum computers. We call these recipes quantum algorithms. Each recipe must guarantee that at the end of the calculation we don’t have a complicated, entangled state that breaks during the measurement but a clear measurement result. There are actually not very many quantum algorithms yet. I will explain in more detail how they basically work in the next part “From classical to quantum computers”.
What do we need for a quantum computer?
We have already found some criteria that we need to build a quantum computer. In 2000, the American physicist David DiVincenzo, who was then working at IBM (now RWTH Aachen), summarised all the conditions that a quantum computer must fulfil. Together they bear the name DiVincenzo criteria:
DiVincenzo criteria
- You need a collection of qubits, i.e. quantum systems consisting of two easily separable states.
- It must be possible to bring each qubit into a fixed initial state.
- The qubits must be stable long enough to perform operations.
- We must be able to perform all the necessary computational operations on the qubits.
- We must be able to read out the qubits.
1. You need a collection of qubits, i.e. quantum systems consisting of two easily separable states.
We have already seen what qubits are in the last article in “What are qubits?” The addition “of two easily separable states” refers to the fact that we must be able to distinguish the two states (0 and 1) of the qubit. If the two states are so close together that we cannot tell them apart, they are useless.
2. It must be possible to bring each qubit into a fixed initial state.
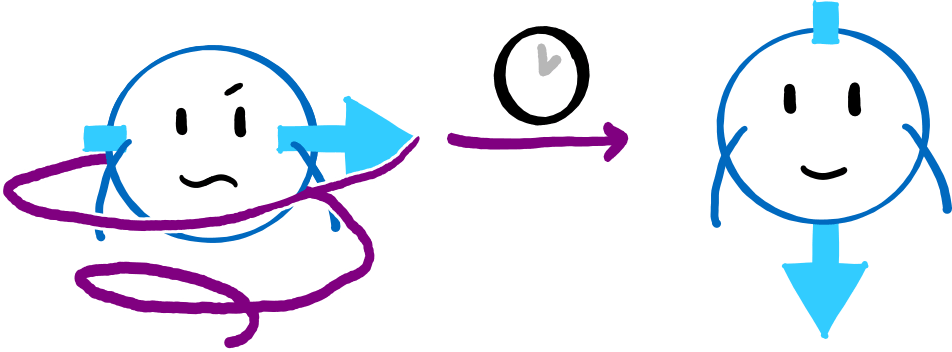
At the beginning of each calculation, we need to know the position of the qubit’s arrow. Often, we start a calculation in the state 0, which means that we have to make sure that our qubit is actually in the state 0 at the beginning of the calculation and nowhere else.
3. The qubits must be stable long enough to perform operations.
A bit, i.e. a switch, stays in its position forever if no one comes and flips it around. A qubit, on the other hand, is vulnerable. If we remember the happy/angry friends: nobody stays angry forever. Eventually, the qubit becomes happy all by itself. And even the precious superpositions and entanglements decay with time. So we have to finish our calculations before the qubits leave their state or the entanglement decays.
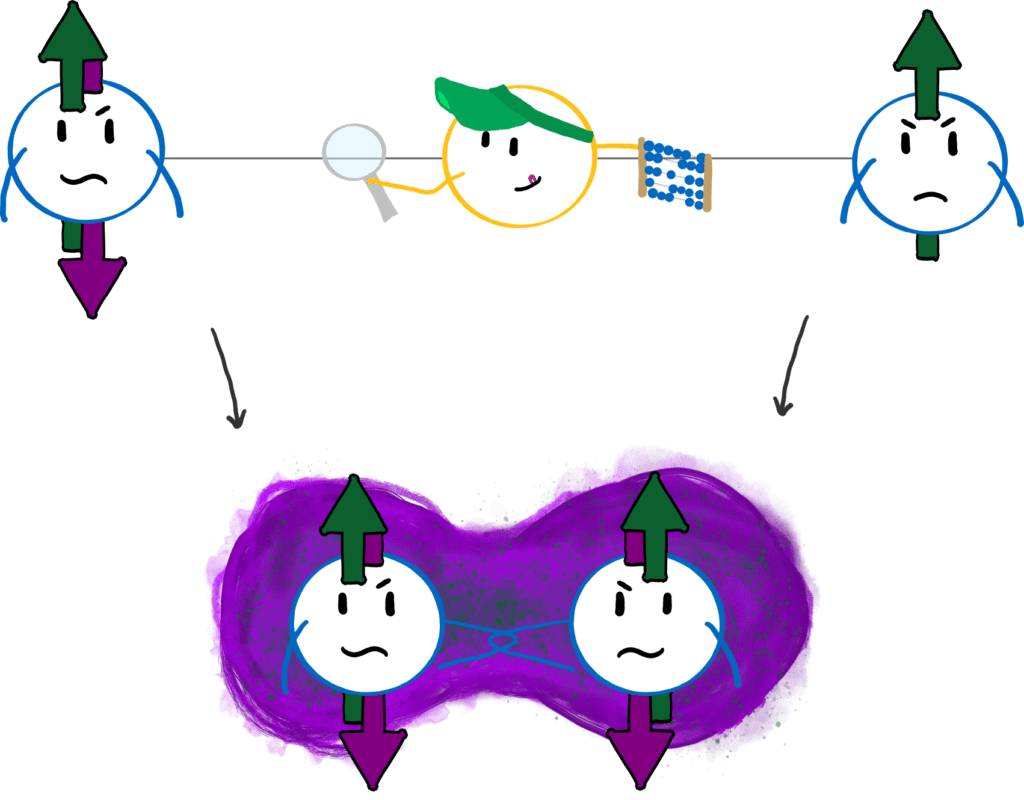
4. We must be able to perform all the necessary computational operations on the qubits.
We have hardly talked about the operations yet. In a normal computer, we call them logical gates and they determine how the switches should be flipped back and forth. We need the same for quantum computers and here we just call them quantum gates. These can act on single qubits or on multiple qubits at the same time.

An example of a quantum gate that acts on two qubits is the CNOT gate, which stands for “controlled not”. This performs the following operation: If qubit A is in state 1, flip the state of qubit B. If not, do nothing. The CNOT gate creates entanglement, because if qubit A is in a superposition of 0 and 1, then the state of qubit B depends on the state of qubit A. If we have such an entangling gate, plus methods to manipulate individual qubits, then we can basically do anything we want!
5. We must be able to read out the qubits.
We have already touched on the last point in the last article in “How to translate quantum information into classical”. In order to read information out of the qubits, we need to be able to measure the state of qubits If we can’t do that, we can’t get the results from the quantum computer. We need a translator to translate the quantum information into classical one.
Why is it so hard to build a quantum computer?
Google, IBM, Microsoft and similar giants are working on the problem – why is there still no fully functional quantum computer? Simply put: Because it’s damn difficult. The biggest problems are:
Stability
Quantum systems are sensitive. As we have already seen in the 3rd DiVincenzo criterion, qubits lose their quantum properties over time. This is because quantum systems constantly interact with their environment: air, radiation and even heat. It’s as if our measurement is constantly screaming at the qubit, constantly reducing it to a bit. This is also why we don’t observe quantum effects in everyday life: They simply break down too quickly.
The loss of quantum information is inevitable. However, we can do two things to deal with it. First, we can try to protect the qubits so that they last as long as possible before the precious quantum information stored in them is lost. But you can never completely protect qubits from their environment. The alternative is therefore to be fast. If we finish our calculation before the quantum information is destroyed, we’re good!
Control
For the 4th DiVincenzo criterion, we need to be able to manipulate the states of qubits. It is easy to flip a switch, but it is very difficult to accurately “flip” qubits. It is even more difficult to manipulate one qubit in dependence on another, especially if the two qubits are far apart. All quantum gates are error-prone – that is, with some probability, the gate will make an error. To perform accurate computation, we need to keep the error of quantum gates as small as possible.
It is not only the quantum gates that make errors but also the measurements. Sometimes the quantum information is difficult to read out, so errors occur. Sometimes qubits are too close to each other to distinguish them well. “Communication difficulties” occur even in the best quantum relationship….
Scalability
We have already established that one qubit is not enough (see “Is one qubit better than one bit?” in the last article). In fact, two qubits are not enough either. To really do something meaningful with a quantum computer, we need more like 50 qubits. If we have a collection of qubits we need to be able to make all the qubits talk to each other. Be it two neighbours or the first and last qubit of a chain.
If we work with “artificial” qubits, such as superconducting qubits, then the mere presence of the other qubits is a source of errors. If two qubits are not completely identical, a kind of noise arises because quantum gates influence them in different ways. The more qubits, the worse this problem is.
Also, with some types of qubits, such as atoms, it can be difficult to keep the qubits in place. Lastly, almost all platforms do not naturally consist of two states, and these undesirable, additional states often pose a problem. If my qubit can be not only happy or angry but also bored – what happens during my calculation? The answer is usually: Nothing good.
We have now talked a lot about how to build a quantum computer and what the difficulties are. But there is one question we have not yet answered: Why? To simulate relationship problems? I don’t think billions would go into researching quantum computers for that. Will quantum computers one day replace classical computers? When will the iPhone 1Q finally arrive? Stay tuned for the next and last part of the series on quantum computers!
Do you want to know how it continues? Then subscribe to my blog and never miss a new post again! Do you like what you read? Then you can buy me a coffee here!
References
David P. DiVincenzo – The Physical Implementation of Quantum Computation