Quanta are sensitive little beings. Under the influence of peer pressure, they behave completely differently when someone is watching. In the last article, I showed you some examples of the so-called observer effect (if you don’t know this part yet, you should urgently read it again).
Quantum mechanical measurements behave completely differently from classical measurements, i.e. the ones we know from everyday life. That’s what we’re going to talk about today: The pitfalls and subtleties of quantum mechanical measurement – and why they are so fascinating!
Basic terms of measurement
First, let’s clarify some basic terms and summarise some initial findings that we already found out in the last article.
What does “measure” mean?
In everyday life, it is a very intuitive term: put on a ruler, turn on a measuring device. In the case of the ruler, we compare a quantity (the length) with a reference (the length measurement on the ruler). In most other cases, however, we do not measure the quantity directly, but couple it to another quantity and it is this quantity that we then measure.
Think of an analogue kitchen scale. You don’t actually measure the weight of the flour. There is a spring in the scale, it is compressed and this deflects a needle. So you couple the weight of the flour to the restoring force of the spring and then measure its deflection.
The same thing happens in most measuring devices. And it’s the same way we do it in quantum physics. Instead of measuring whether my atom is in state A or B (which I have no direct access to, I can’t see them), I couple the atom to something else and then measure that quantity. This is called indirect measurement.
Observation means measurement
As soon as you enter the world of quantum physics, you will notice that the terms “observe” and “measure” are used almost as synonyms. We assume that just looking is enough to measure something. In the normal world, this is strange: just because I look sharply at the flour, I still don’t know how much exactly it is now.
But quantum objects are sensitive, as we already know, and usually just looking at them is enough to disturb the system. This is because quantum systems are usually sealed off in experiments: in high vacuum, cryostats, protected from radiation and any outside influence. As soon as we “look”, we have to open the system – and thus we automatically introduce disturbances, and that is effectively the same as measuring the system.
Measurement results are statistically distributed
No one can predict what the outcome of a measurement will be – not even the quantum object itself, if we could ask it. Let’s take a qubit as an example. We know that qubits are less like switches (0 or 1) and more like balls (0 or 1 and everything in between). Now when I measure “Are you in 1?” my measurement result depends on where my qubit pointer is pointing at the time of the measurement.
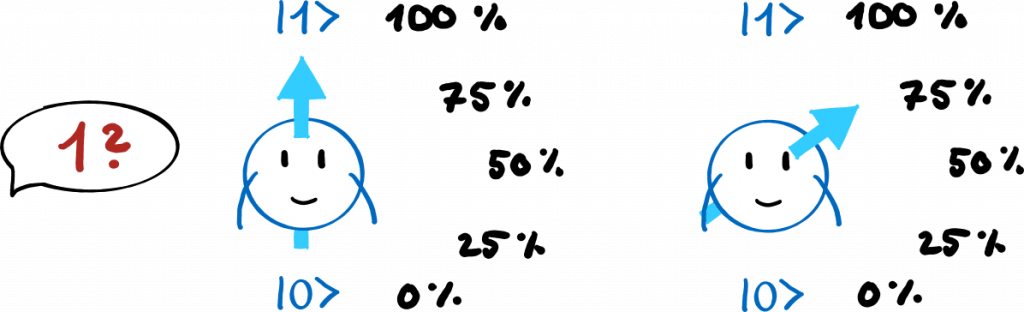
The measurement of one property influences another
Heisenberg’s uncertainty principle tells us that we cannot know two related quantities with arbitrary precision at the same time. The prime example of this is the location and the velocity (more precisely: momentum, i.e. mass times velocity) of a particle.
But if I measure a quantity, for example, the location, I know it exactly. What happens to the momentum then? It smears apart! In other words, I no longer have any idea how fast my particle is.
This also works with the qubit. If I measure the property “0 or 1”, the matching property that I smudge is the azimuth angle of the arrow in the equatorial plane (the red one). Because if the arrow points up or down, it no longer has an angle in the plane.

Measurements break quantum properties
So when I make a measurement, my qubit effectively goes from a sphere to a switch – it behaves like an ordinary, classical bit after the measurement. In other words, measurements make quantum systems classical. This is, roughly speaking, because measurements work like translators from the quantum world to the classical world. A measurement result must be classical for us to understand it. But the quantum state is quantum mechanical. In order for this to fit together, the measurement must “make the quantum system classical”.

Measurements cannot be reversed
This is a direct consequence of the previous point. Once quantum properties are erased, they cannot be brought back. This “flattening” is also called collapse of the wave function; the wave function is the mathematical object we use to describe quantum states. This object collapses into something smaller: The zombie cat becomes a house cat, the qubit becomes a bit.
After that, there is no going back. Of course, we can start all over again, put the cat back in the box and re-superimpose the qubit, but we cannot recover the lost information.
The marble and the quantum blob
Let’s look at a concrete example to better understand this collapse.
Imagine you have a normal, classical system: a marble. The marble can be in different compartments of a box: 1 to 5. These are the five different measurements. Whether we look or not, the marble is always above or in one of the five compartments.
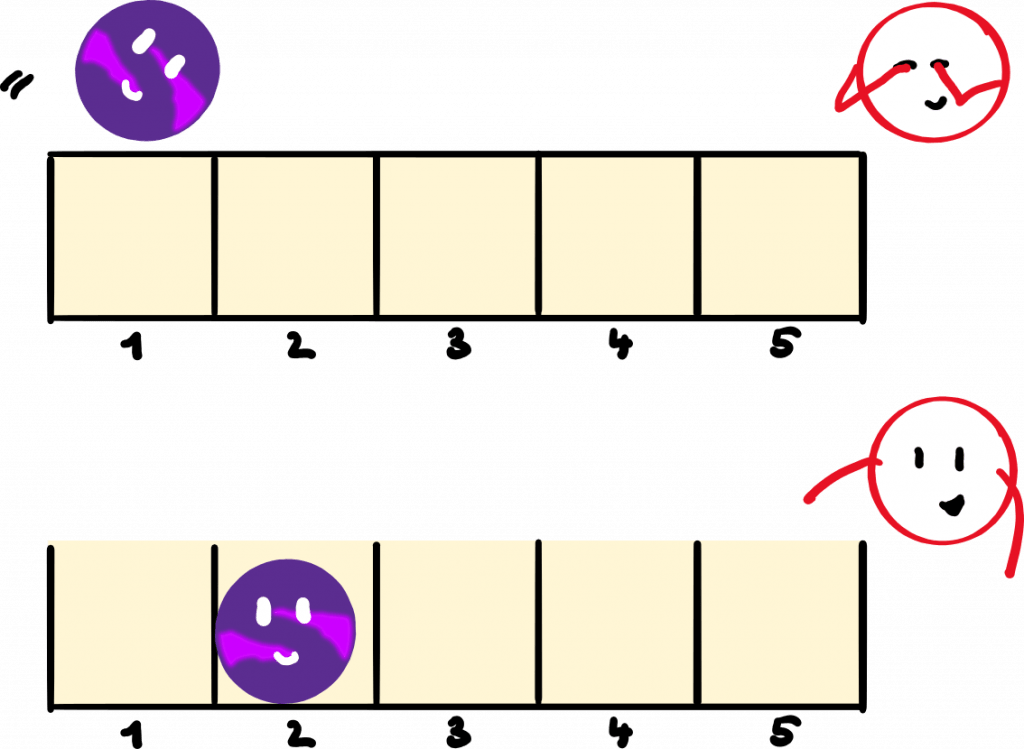
A quantum system is not a marble, but a slimy blob. As long as no one is looking, the blob happily smears itself across the five compartments. But when we look and measure which compartment the blob is in, the poor blob collapses in fright and falls into one of the compartments.
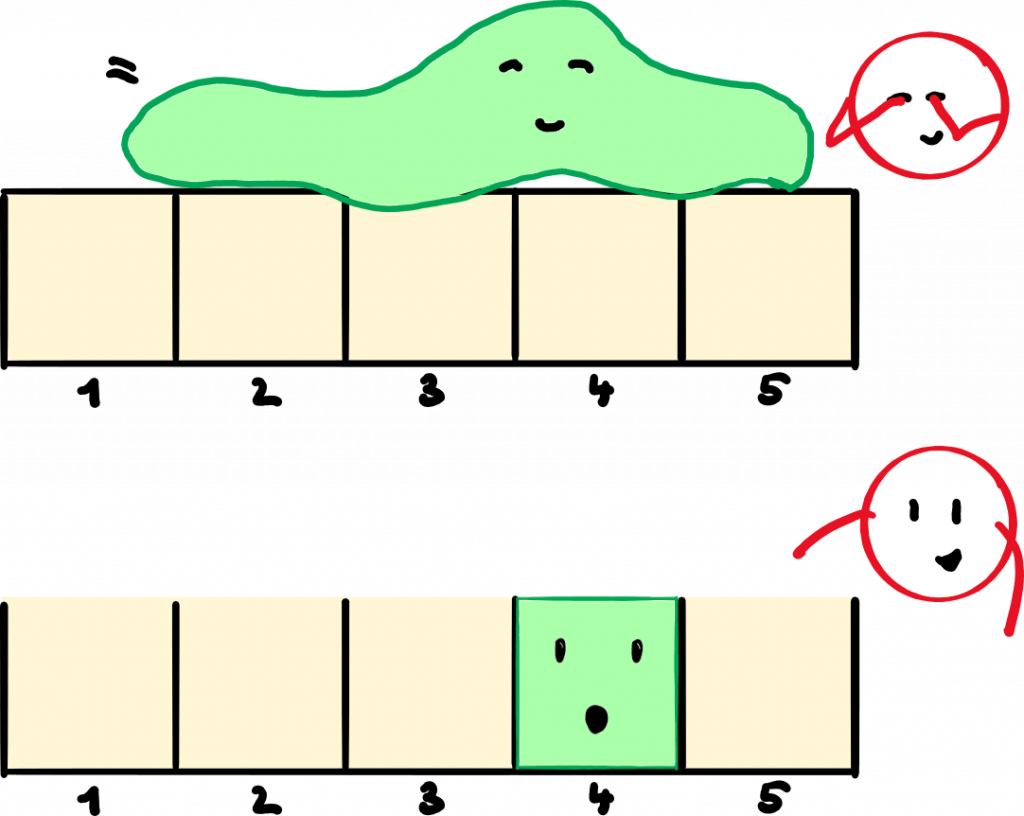
You guessed it: the quantum blob is our wave function. From it, we can calculate the probability with which our quantum system is at which location. From our observations above, we can now deduce the following:
- It is most likely that the blob will fall into the compartment that had the most slime on top of it at the moment of looking. The second most likely is the compartment with the second most slime mass, and so on.
- Even with two completely identical slime distributions, the blob may fall into different compartments. The same thing will not happen every time.
- It follows: We cannot predict which compartment the blob will fall into, even if we know its slime distribution. (Exception: the entire blob is above a compartment).
- Once the blob has fallen into a compartment, we can no longer reconstruct what the slime distribution was before the collapse.
Where is the problem in the measurement problem?
The article is called: “The Measurement Problem in Quantum Mechanics”. So you can now ask: Where is actually the problem?
The discontinuity of measurement
All the rest of quantum mechanics is continuous, that is given by the Schrödinger equation. Why then does the measurement collapse so abruptly? Why is it irreversible, i.e. not reversible, while every other development can be reversed? And when exactly does the collapse actually happen? When I look at the measuring device? When the measuring device is connected?
Let’s admit it: the measurement is weird and completely different from anything else in quantum mechanics. We have found a mathematical formalism that works and can statistically describe the output of measurements. But we don’t really understand what is happening and why.
What is the wave function?
The wave function is a mathematical tool to describe the outcome of experiments. It can do that quite well – quantum physics is now the best-tested theory in all of physics. But the wave function is not real, which means I can’t touch it and I can only measure it indirectly. What is that supposed to mean??
This question has given rise to various interpretations of quantum physics (I have presented a few of them here). They all deal with the measurement problem differently. But they all are and remain: interpretations, philosophy. What this abstract object we reckon with every day is supposed to be, we don’t know. But I have a feeling we will see the quantum blob again!
This is the second part in the series “Quanta are watching you”. To make sure you don’t miss a post, don’t forget to subscribe to my blog. If you like what you read, you can buy me a coffee here.


