Der Quantencomputer als heiliger Gral: Mit ihm wird alles besser, alles schneller, unlösbare Probleme werden zum Kinderspiel, Banken nehmt euch in Acht – eure Verschlüsselung ist am Ende! Ist das wirklich so? Worin sind Quantencomputer wirklich besser als klassische Computer und worin vielleicht nicht? In meiner Serie „FAQ: Quantencomputer“ versuche ich häufige Missverständnisse zu beseitigen und Fragezeichen wegzuwischen.
Das FAQ besteht aus drei Teilen. Im ersten Teil, „Vom Bit zum Qubit“, erklärte ich die grundlegenden Unterschiede zwischen klassischen Bits und quantenmechanischen Qubits. Im zweiten Teil „Vom Qubit zum Quantencomputer“ ging es darum, was man für einen Quantencomputer braucht und was ihn so mächtig macht. Falls du sie noch nicht kennst möchtest du vielleicht mit den ersten beiden anfangen, weil ich mich auf sie beziehen werde. Dies ist der letzte Teil der Serie und hier geht es um die Unterschiede von klassischen und Quantencomputern. Rechnen Quantencomputer genauso wie klassische Computer? Wie funktionieren Quantenalgorithmen? Was können Quantencomputer besser als normale? Was können normale Computer besser als Quantencomputer? Wie viele Qubits hat ein Quantencomputer? Gibt es Quantencomputer nicht schon? Wann wird es Quantencomputer für zu Hause geben?
Rechnen Quantencomputer genauso wie klassische Computer?
Theoretisch können sie das. Normale Computer flippen die Zeigerstellungen von Bits mithilfe von logischen Gattern um. Aus 0 mach 1; aus 1 mach 0; aus 1 mach 0, aber nur wenn links davon auch eine 1 steht; und so weiter. Mithilfe von Quantengattern können wir auf Quantencomputern genau das gleiche machen (siehe auch „Was braucht man für einen Quantencomputer?“ im letzten Artikel). Allerdings ist das auf Quantencomputern sehr viel schwieriger als auf normalen, und in der Regel ist das Ergebnis unzuverlässiger.
Oft wird der Eindruck erweckt, ein Quantencomputer könne Probleme schneller lösen, indem einfach alle möglichen Ausgangssituationen überlagert werden, weil „Superposition und so“. Das klappt aber nicht, weil wir das Ergebnis am Ende auch auslesen können müssen. Und genau das ist ziemlich kompliziert, weil Qubits vom Auslesen selbst beeinflusst werden. Dadurch geht Quanteninformation kaputt, wenn wir nicht genau aufpassen (siehe „Kann ein Quantencomputer jedes Problem in einem Schritt lösen?“ im letzten Artikel).
Das Fazit: Wir können Probleme nicht genauso lösen wie zuvor und hoffen, dass es mit einem Quantencomputer schneller geht. Um Qubits für effizientes Computing zu benutzen ist radikales Umdenken notwendig. Wir müssen uns für jedes Problem eine passende Quanten-Lösung überlegen. Nur wenn diese Lösung klug designt ist und den Quanten-Parallelismus effizient ausnutzt ist ein Quantencomputer schneller als ein normaler. Diese Quanten-Lösungen sind wie Kochrezepte, die uns Schritt für Schritt erklären, wie wir das Problem lösen, und wir nennen sie Quantenalgorithmen. Ein Quantenalgorithmus muss garantieren, dass wir am Ende einer Rechnung keinen komplizierten, verschränkten Zustand haben, der bei dem Auslesen kaputt geht, sondern ein klares Messergebnis. Die traurige Wahrheit ist: So richtig viele Quantenalgorithmen kennen wir noch gar nicht. Ein Beispiel zeige ich euch jedoch in der nächsten Frage.
Wie funktionieren Quantenalgorithmen?
Jeder Quantenalgorithmus ist anders und es wäre unmöglich, die Funktionsweise jedes Quantenalgorithmus‘ gleichzeitig zu erklären. Deshalb beschränke ich mich auf ein konkretes Beispiel.
Stell dir vor, du möchtest einen Namen auf einer unsortierten Liste finden. Da die Namen willkürlich auf der Liste angeordnet sind, bleibt dir nichts andere übrig, als die Liste von oben nach unten durchzusehen. Im Schnitt findest du den gesuchten Namen nach etwa der Hälfte der Liste; im schlimmsten Fall musst du die Liste ganz bis zum Ende lesen.
Geht das nicht besser? Aber ja, mit Quantenphysik! Genauer gesagt mit einem Quantenalgorithmus, wie Lov Grover 1996 zeigte. Er bewies, dass sein Quantenalgorithmus den Namen in weniger Schritten finden kann als ein klassischer Algorithmus. Wenn man eine Liste der Länge 
betrachtet, braucht man nur etwa 
Schritte – ein erheblicher Vorteil, wenn die Liste sehr lang ist! Der Grover-Algorithmus ist tatsächlich der bisher einzige Quantenalgorithmus, der bewiesenermaßen besser ist als sein klassisches Pendant. Es gibt noch andere Quantenalgorithmen, die schneller sind als die bekannte, klassische Lösung (zum Beispiel die Primfaktorzerlegung mithilfe des Shor-Algorithmus) – es könnte jedoch einfach sein, dass man die beste klassische Lösung einfach noch nicht gefunden hat. Nicht so für den Grover-Algorithmus!
Der Grover-Algorithmus ist kompliziert und besteht aus komplexen Quantenoperationen. Doch für vier Elemente kann man die Grundidee des Algorithmus ganz gut veranschaulichen (Vorsicht: es wird trotzdem etwas technisch). Wir erinnern uns, dass man mit zwei Qubits vier Elemente darstellen kann – wie praktisch! Wir brauchen also lediglich zwei Qubits um Frodo in der Hobbit-Liste zu finden, und das in nur einem einzigen Schritt! Los geht’s:
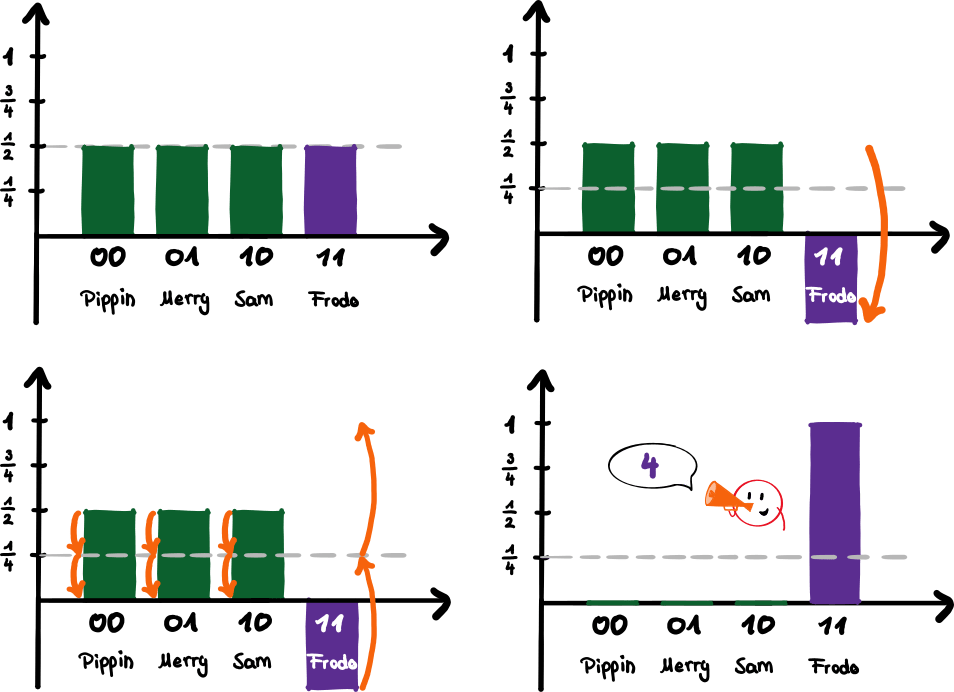
Ausgangssituation: Wir tappen im Dunkeln
Wir stehen am Anfang und haben keine Ahnung, wo Frodo ist (Bild oben links). Das bedeutet, die Wahrscheinlichkeit Frodo zufällig in der Liste zu finden ist 25%. Genauso hoch ist die Wahrscheinlichkeit für die anderen Hobbits. Ein Wort zum Balkendiagramm im Bild: Die y-Achse (die, die nach oben zeigt), gibt nicht die Wahrscheinlichkeit an, einen Namen auf der Liste zu finden. Stattdessen zeigt sie den quantenmechanischen „Vorfaktor“ der vier Zustände 00, 01, 10, 11 an. Wenn diese Zahl quadriert wird erhalten wir die Wahrscheinlichkeit, diesen Zustand zu messen 
. Das tun wir jetzt aber noch nicht!
1. Schritt: Spiegelung von Frodo
Mithilfe einer Quantenoperation können wir das Vorzeichen des gesuchten Elements umdrehen (Bild oben rechts; die y-Achse zeigt also definitiv keine Wahrscheinlichkeiten an, da der Wert nun negativ ist und negative Wahrscheinlichkeiten gibt es nicht). Damit haben wir Frodo aber noch nicht gefunden, da die Wahrscheinlichkeit Frodo zu messen noch immer 25% ist 
. Mithilfe der Quantenphysik können wir aber in die Liste „hineinfühlen“ – die zwei Qubits spüren Frodo bereits. Wir können mit dieser Information aber nichts anfangen.
2. Schritt: Spiegelung aller Hobbits
Nun spiegeln wir alle vier Säulen (Bild unten links). Jedoch nicht an der x-Achse (die, die nach rechts zeigt), sondern am Mittelwert der vier Säulen (der grauen, gestrichelten Linie). Da Frodo negativ ist, ist der Mittelwert der vier Amplituden 
. Die Spiegelung ist durch die orangefarbenen Pfeile verdeutlicht.
Frodo offenbart sich
Die Spiegelung hat uns ans Ziel geführt (Bild unten rechts)! Die Amplitude von Pippin, Merry und Sam ist nun 0, die von Frodo ist 1. Wenn wir die zwei Qubits nun auslesen werden wir mit 100% Wahrscheinlichkeit Frodo finden!
Es ist jedoch nicht immer so einfach, wie in diesem Beispiel mit vier Einträgen. Deshalb jetzt noch ein paar Anmerkungen für die, die es genau wissen wollen:
- „Wieso nennst du das einen Schritt, waren das nicht mehrere Schritte?“ Ja, das ist eine Frage der Definition. Wir haben oben zwei Operationen durchgeführt (die zwei Spiegelungen) und eine Messung (der letzte Schritt). Tatsächlich sind zur Ausführung der zwei Spiegelungen auf einem echten Quantencomputer sogar mehrere Quantengatter nötig. Das alles kann jedoch als eine komplexe Operation interpretiert werden. Und genau diese wird bei einer längeren Liste immer wieder wiederholt. Gemessen wird aber in jedem Fall nur einmal ganz am Ende.
- „Geht das immer in einem Schritt?“ Nur für den Fall von vier Listeneinträgen kann der Grover Algorithmus das Element in einem Schritt finden. In allen anderen Fallen müssen Schritt 1. und 2. mehrfach wiederholt werden.
- „Moment mal, wieso denn überhaupt ein Schritt? Du sagtest, der Grover Algorithmus benötigt 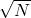Schritte, um das Element zu finden, aber
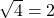und nicht 1!“ Tatsächlich benötigt der Grover-Algorithmus nicht exakt 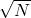Schritte, sondern die Anzahl der Schritte skaliert mit 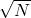. Die Formel 
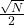skaliert ebenfalls mit 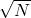und auch die Formel 
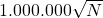skaliert mit 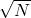. Die Frage ist, um wie viel die Anzahl der Schritte zunimmt, wenn die Liste länger wird. Die genaue Formel für den Grover Algorithmus ist etwas komplizierter, doch der Faktor 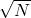kommt darin vor. Für drei Qubits, also 
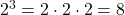Listeneinträge, werden 1-2 Schritte benötigt, für fünf Qubits (
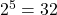Einträge) gerade einmal vier! - „Wie macht man diese Spiegelungen?“ In einem Diagramm sehen sie recht anschaulich aus, doch müssen wir die Qubits dazu bringen, sich genau so zu verhalten. Das machen wir mithilfe von Quantengattern. Ganz praktisch heißt das: Wir schießen zum Beispiel elektromagnetische Pulse auf die Qubits, um deren Pfeile in einer ganz bestimmten Art und Weise zu drehen.
- „Haben alle Quantenalgorithmen irgendetwas gemeinsam?“ Das Grundkonzept, auf dem alle Quantenalgorithmen basieren, ist die Interferenz (mehr dazu hier), also die Überlagerung von Materiewellen: Die „schlechten“ Listeneinträge interferieren destruktiv, sodass ihre Amplituden irgendwann (nahezu) Null werden. Der „gute“ Listeneintrag interferiert konstruktiv, sodass seine Amplitude (nahezu) Eins wird. Das sieht man gut anhand der zweiten Spiegelung: sie hebt die schlechten Einträge einfach auf und verstärkt den guten.
Was können Quantencomputer besser als normale?
Grob gesagt sind Quantencomputer normalen immer dann überlegen, wenn man die Lösung durch bloßes Raten und Ausprobieren finden könnte. Elemente in einer Liste finden, Zahlen in ihre Faktoren zerlegen, Passwörter knacken, Sachen optimieren. Die Deutsche Bahn zum Beispiel hofft in der Zukunft ihre Streckennetze mit Quantencomputern zu optimieren (was sie auch dringend nötig hat).
Es gibt eine Sache, die ein Quantencomputer kann, die ein klassischer Computer nicht kann: Zufallszahlen generieren. Vielleicht wundert euch das, denn selbst im Internet gibt es Zufallszahlengeneratoren. Das scheint doch kein Problem zu sein? Nicht so ganz, denn es ist tatsächlich eine super schwierige Aufgabe, komplett und perfekt zufällige Zahlen zu generieren.
Im Alltag ist es gar nicht so schwierig, Zufallszahlen zu erzeugen: man nehme zum Beispiel eine Münze oder ein Würfel. Wenn man genau hinguckt ist das Ergebnis aber nicht zufällig: Wenn ich alle äußeren Parameter des Würfelwurfs kenne, kann ich das Ergebnis berechnen. Ich brauche dafür nur die Kraft, mit der ich den Würfel werfe, das Material des Würfels und des Tischs, die Lage des Würfels in meiner Hand, der Winkel mit dem ich werfe, die Windgeschwindigkeit, die Temperatur, die Sternenkonstellation, … Ähm, ja. Ihr seht, in einen einfachen Würfelwurf fließen so viele Parameter ein, die wir in der Praxis nicht genau genug kennen, sodass es unmöglich ist, das Ergebnis exakt vorherzusagen. Deshalb können wir mit gutem Gewissen sagen: das Ergebnis ist zufällig.
Wie aber macht ein Computer das? Ein Computer hat keinen Würfel. Computer sind dazu designt Rechenvorschriften auszuführen: Nimm A und mach B damit, und dann nenne mir das Ergebnis C. Ein Computer ist überfordert mit der Aufgabe: Mach was du willst, sag es mir aber nicht, und dann nenne mir das Ergebnis. Deshalb sind Zufallszahlen von Computern nur pseudo-zufällig. Die Zahlen sehen zufällig aus, tatsächlich steckt aber eine komplizierte Rechenvorschrift dahinter, die vorhersehbare Zahlen ausspuckt.
Ein Quantencomputer ist aber anders. In der Quantenphysik können wir den Zustand eines Qubits nur mit einer gewissen Wahrscheinlichkeit vorhersagen. Ein Qubit in einer Superposition aus den Zuständen 0 und 1 gibt mit 50% Wahrscheinlichkeit den Zustand 0 und mit 50% Wahrscheinlichkeit den Zustand 1 zurück. Tada: unsere 100% zufällig Quantenmünze! Mit nichts in der Welt können wir das Ergebnis dieses Münzwurfs vorhersagen.
Was können normale Computer besser als Quantencomputer?
Grob gesagt: Alles andere (also außer Elemente in einer Liste finden, Zahlen in ihre Faktoren zerlegen, Passwörter knacken, Sachen optimieren,…). Wenn wir keinen Quantenalgorithmus kennen, der ein Problem mit Quantenpower löst, dann ist ein Quantencomputer nutzlos. Wie oben erklärt können Quantencomputer im Prinzip alles, was klassische Computer auch können – nur schlechter.
Es gibt ein Beispiel für eine Sache, die Quantencomputer aber tatsächlich nicht können: Kopieren. Eines der wichtigsten Resultate der Quantenphysik ist das No-Cloning-Theorem. Es besagt, dass es unmöglich ist, ein beliebiges Qubit zu kopieren. Um den Zustand eines Qubits zu kopieren, muss ich erstmal wissen, was dieser Zustand eigentlich ist. Bei klassischen Bits ist das ganz einfach: Ich schaue mir ein Bit an (Zeigt der Schalter nach oben oder unten?) und flippe den Schalter eines anderen Bits in genau die gleiche Position – erledigt. Dieses „Anschauen“ ist bei Qubits aber nicht so einfach, da das bloße Angucken das Qubit in der Regel beeinflusst. Die einfache Zuweisung a = b ist auf einem Quantencomputer nicht möglich.
Das klingt ziemlich hinderlich, wenn man einen Computer bauen will. Tatsächlich ist genau diese Eigenschaft aber der Schlüssel für die Quantenkryptographie! Ein Ziel der Quantenkryptographie ist es, Nachrichtenübertragung unabhörbar zu machen. Wenn Spitzel normale Nachrichten abhören wollen, fangen sie sie ab, lesen die Nachricht und schicken sie (oder eine Kopie davon) weiter. Der Empfänger kann nie genau wissen, ob ein Spitzel die Nachricht abgehört hat. Quanten-Nachrichten sind vor solchen Überfällen ganz natürlich geschützt, weil sie weder unbeschädigt gelesen noch kopiert und weitergeschickt werden können.
Wie viele Qubits hat ein Quantencomputer?
Den Rekord für die höchste Anzahl an Qubits hält derzeit Google mit 72. IBM liegt mit 65 knapp dahinter – die beiden wechseln sich regelmäßig ab. Die eigentlich relevante Frage ist jedoch: Wie viele Qubits brauchen wir, um nützliche Dinge zu tun? Gegenfrage: Was ist nützlich?
Das Paradebeispiel für Quantencomputer ist das Knacken von Verschlüsselungen. Das wichtigste Verfahren ist die RSA-Verschlüsselung, die für Kreditkarten, E-Mails, auf Reisepässen und für noch viel mehr verwendet wird. Sie basiert, einfach gesagt, auf der Primfaktorzerlegung: Während es noch einfach ist, kleine Zahlen wie die 15 in die Faktoren 3 und 5 zu zerlegen, ist für eine Zahl mit mehreren hundert Stellen ein enormer Rechenaufwand nötig. RSA-2048 verwendet 2048 Bits zur Verschlüsselung, was in einer Zahl mit 617 Stellen resultiert. Eine so große Zahl in ihre Primfaktoren zu zerlegen würde auf einem klassischen Computer 300 Billionen Jahre dauern – es ist also nicht zu viel gesagt, dass dies als unmöglich gilt. Hätte man hingegen einen Quantencomputer mit knapp 4000 perfekten Qubits könnte man den Code in 10 Sekunden knacken.
Deshalb hat sich bereits ein weiteres Forschungsgebiet entwickelt: Die Post-Quanten-Kryptographie. Denn sobald wir einen 4000 Qubit-Quantencomputer haben sind unsere Kreditkarten ungeschützt. Es ist der Kreis des Lebens: Wir lösen Probleme und schaffen damit direkt neue, die wir lösen müssen.
Gibt es Quantencomputer nicht schon?
Wenn man es genau nimmt: Ja. Es sind jedoch noch nicht die übermächtigen, Code-brechenden Maschinen, von denen alle Träumen. Heutige Quantencomputer lassen sich in drei Kategorien einteilen:
Adiabatische Quantencomputer
Wenn man die Website der kanadischen Firma D-Wave Systems öffnet liest man zuallererst die Worte „Der erste und einzige Quantencomputer gebaut für Unternehmen“. Klare Ansage. Bereits 2011 behauptete die Firma, den ersten kommerziellen Quantencomputer entwickelt zu haben. Sie verkauften ihr Gerät D-Wave One für 10 Millionen US$. Der Teufel steckt jedoch im Detail, denn das Gerät ist kein Quantencomputer in dem Sinne, wie ich ihn hier benutze. Er funktioniert nicht mit Quantengattern und kann mit den üblichen Quantenalgorithmen nichts anfangen. Obwohl das neuste Gerät D-Wave Advantage 5760 Qubits hat brauchen wir also noch nicht um unsere Sicherheit zu fürchten – für die Primfaktorzerlegung mit Shors Algorithmus braucht man einen „richtigen“ Quantencomputer. Die D-Wave Geräte sind stattdessen sogenannten adiabatische Quantencomputer. Das Funktionsprinzip ist folgendermaßen:
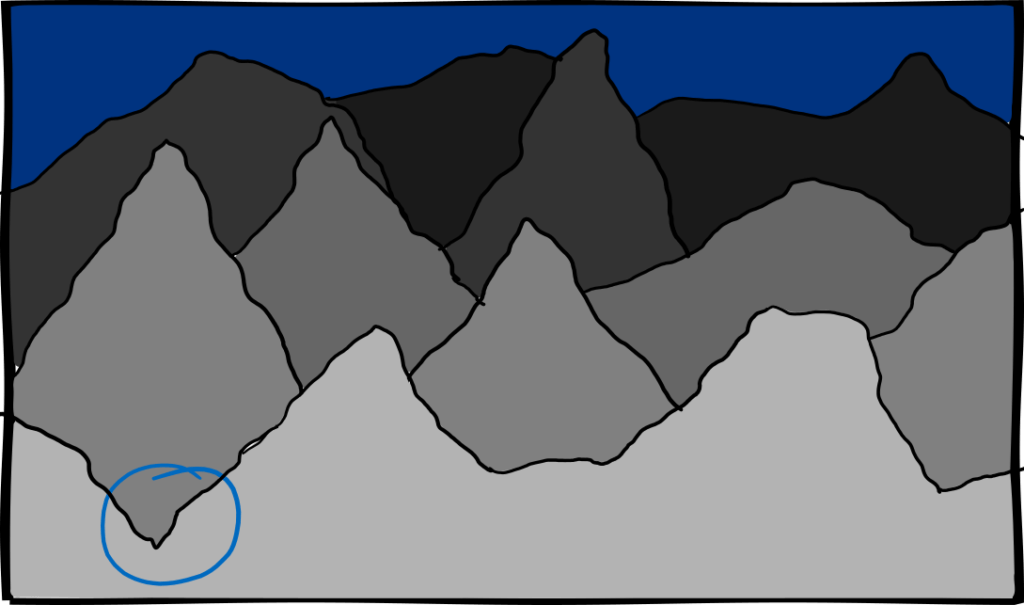
Mithilfe von adiabatischen Quantencomputer lassen sich Optimierungsprobleme lösen. Das heißt, man versucht das Minimum oder Maximum eines Prozesses zu finden. Eine Optimierung kann man sich als bergige Landschaft vorstellen, und das Ziel ist es, den tiefsten Punkt zu finden. Nehmen wir an wir haben das Modell der Landschaft in einer Kiste vor uns. Ein adiabatischer Quantencomputer schaut sich dann jeden Punkt gleichzeitig an, indem er (bildlich gesprochen) Puderzucker auf der Landschaft streut. Dann schütteln wir die Kiste vorsichtig, bis sich der gesamte Zucker am tiefsten Punkt sammelt. Wichtig ist es die Kiste langsam und sachte zu schütteln, denn „adiabatisch“ ist ein physikalischer Fachbegriff für „super langsam„: Schütteln wir zu hart, kann der Zucker über kleine Unebenheiten hinweg springen und landet nicht am tiefsten Punkt. Quantenzucker hat außerdem den Vorteil, dass er durch Berge hindurch springen kann, wenn er merkt, dass es auf der anderen Seite weiter nach unten geht. Das nennen wir tunneln. Deshalb sind adiabatische Quantencomputer super geeignet, um Optimierungsprobleme wie dieses zu lösen.
Quantencomputer der NISQ-Ära
Das chinesische Unternehmen SpinQ Technology sagt auf seiner Website „Gemini ist der erste kommerziell erhältliche Desktop-Quantencomputer der Welt.“ Klingt toll, und kostete nur US$50.000. Die nächste Generation, die Ende des Jahres rauskommen soll, soll sogar nur $5.000 kosten. Liest man etwas weiter findet man jedoch den Zusatz „Es bietet eine umfassende Lösung für die Lehre und Demonstration von Quantencomputern.“ Denn der SpinQ Gemini besteht aus nur zwei Qubits. Codes knacken kann man damit eher nicht (aber Frodo kann man finden!)
Wie oben beschrieben benötigen wir 4000 Qubits zum Knacken der besten Verschlüsslung. Doch bereits mit ein paar Dutzend perfekten Qubits könnte man relevante Probleme lösen (es muss ja nicht immer direkt das Brechen des globalen Hochsicherheits-Verschlüsselungssystems sein). Das Problem ist nur: heutige Qubits sind alles andere als perfekt. Sie sind instabil und geben mit einer gewissen Wahrscheinlichkeit ein falsches Ergebnis raus. Der Hauptgrund dafür ist die Dekohärenz: der Zerfall von Quanteninformation über die Zeit (siehe „Warum ist es so schwer einen Quantencomputer zu bauen?“ im letzten Artikel).
Wir befinden uns derzeit in einer Grauzone: der sogenannten NISQ-Ära, für Noisy Intermediate Scale Quantum. Das bedeutet, die Anzahl der Qubits ist bereits groß genug (intermediate scale), um komplexe Probleme zu lösen, jedoch werden die Ergebnisse durch Rauschen verfälscht (noisy). Der heilige Gral des Quantencomputing ist ein Gerät mit eingebauter Fehlerkorrektur. Die Idee ist, die Fehler der verrauschten Qubits mithilfe zusätzlicher Qubits zu korrigieren. Wie viele Qubits zur Fehlerkorrektur benötigt werden ist noch unklar, doch vermutet wird ein Verhältnis von 1:10. Da eines der größten Probleme derzeit ist, die Anzahl der Qubits hochzutreiben, sind fehlertolerante Quantencomputer noch nicht realisierbar.
Wenn wir die Fehlerkorrektur mit einbeziehen erhöht sich die Anzahl der Qubits erheblich, um RSA zu knacken. Neuste Rechnung zeigen, dass man 20 Millionen Qubits braucht, um die Verschlüsselung in nur acht Stunden zu knacken. Das ist ein ganzes Stück mehr als 4000, und noch mal sehr viel mehr als die 70 die wir derzeit haben. Vermutlich wird es noch Jahrzehnte dauern, bis wir dort angekommen sind.
Cloud-basierte Quantencomputer
Bereits seit 2016 erlaubt IBM der breiten Öffentlichkeit Zugriff auf seine Quantencomputer – über das Internet. Das Projekt wurde unter dem Namen IBM Quantum Experience gestartet, und kürzlich in die zwei Komponenten IBM Quantum Composer (für die Drag-and-Drop-Erstellung von Quanten-Schaltkreisen) und IBM Quantum Lab (für die Programmierung mithilfe einer für Quantencomputer angepassten Programmiersprache) aufgeteilt. IBM erlaubt Nutzer*innen Zugriff auf ihre Quantenprozessoren mit zwischen einem und 65 Qubits. Diesen Zugriff über das Internet nennt das Unternehmen die IBM Cloud.
Statt einen Quantencomputer zu Hause zu haben können wir also aus der Ferne auf Cloud-basierte Quantencomputer zugreifen. Die Idee ist die gleiche wie bei Cloud Gaming: Spiele werden nicht mehr lokal auf dem eigenen Rechner installiert, sondern auf einem externen Server. Die Tastatur- und Mauseingabe des Gamers wird zum Server geschickt, und der Server schickt Bild und Ton zurück, alles übers Internet.
Der Vorteil davon ist, dass die empfindlichen Qubits sicher verpackt in einem Kryostat oder Vakuum irgendwo weit entfernt in einem Quanten-Serverraum stehen. Es gibt auch Plattformen, die diese extremen Bedingungen nicht brauchen (siehe „Woraus bestehen Qubits?“ im ersten Teil), aber in der Regel sind sie trotzdem besser für die Performance des Quantencomputers. Alle namenhaften Vertreter des Quantum Computing bieten mittlerweile einen Cloud Zugriff an: IBM, Google, D-Wave, Amazon und viele mehr.
Wann wird es Quantencomputer für zu Hause geben?
Ich bin einmal mutig und sage: Vermutlich niemals. Wie in „Was können Quantencomputer besser als normale?“ erklärt, glänzen Quantencomputer hauptsächlich in Bereichen, die man als Otto-Normal-User eher nicht braucht (außer man ist Profi-Hacker oder als freiberuflicher Spion unterwegs). FALLS Quantencomputer doch jemals zu Hause eine Rolle spielen werden, dann ist mein Tipp, dass es über die Cloud passieren wird, da diese Entwicklung bereits begonnen hat. Insbesondere da Forscher*innen schlichtweg nicht daran arbeiten, Heim-Quantencomputer zu entwickeln.
Tatsächlich geht es auch nur entfernt darum, Quantencomputer für die industrielle Produktion zu entwickeln. Wir sind noch immer in der Forschungsphase: Ist es überhaupt möglich, einen Quantencomputer zu entwickeln, der signifikante Probleme lösen kann, die ein normaler Computer nicht (in einer vernünftigen Zeit) lösen könnte? Geräte der NISQ-Ära sind Produkte dieser Forschung, doch sie sind noch nicht das finale Ergebnis. Die meisten Forscher*innen sind zuversichtlich und es klingt nur nach einer Frage der Zeit. Doch bis wir den „heiligen Gral“ tatsächlich in der Hand halten können wir uns nicht sicher sein, ob wir ihn wirklich finden werden.
In diesem Artikel habe ich über den Quantencomputer gesprochen, der nur eine von vielen Quantentechnologien ist. Vielleicht interessiert dich auch der Artikel zur zweiten Quantenrevolution.
Gefällt dir was du liest? Dann abonnier meinen Blog und verpass keinen neuen Beitrag mehr, oder, wenn du möchtest, kannst du mir hier einen Kaffee spendieren!
Quellen
Grover Algorithmus
Breaking RSA Encryption – an Update on the State-of-the-Art
How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits
IBM Quantum Experience
D-Wave Leap
Google Quantum Computing Playground (ehemals http://quantumplayground.net/, abgerufen 04/2022)
Amazon Braket Quantencomputer
SpinQ Gemini: a desktop quantum computer for education and research
SpinQ Website